题目内容
若正数x,y满足x+4y=4,则xy的最大值为 .
1
【解析】由基本不等式可得x+4y≥2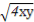 =4
=4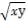 ,于是4
,于是4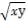 ≤4,xy≤1,当且仅当x=2,y=
≤4,xy≤1,当且仅当x=2,y=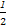 时取等号,故xy的最大值为1.
时取等号,故xy的最大值为1.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
题目内容
若正数x,y满足x+4y=4,则xy的最大值为 .
1
【解析】由基本不等式可得x+4y≥2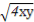 =4
=4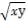 ,于是4
,于是4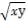 ≤4,xy≤1,当且仅当x=2,y=
≤4,xy≤1,当且仅当x=2,y=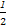 时取等号,故xy的最大值为1.
时取等号,故xy的最大值为1.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案