题目内容
(本小题满分14分)已知函数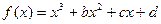 在(0,+
在(0,+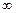 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程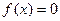 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.
(1)求c的值;
(2)求证: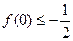 ;
;
(3)求|α–β|的取值范围.
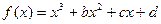 在(0,+
在(0,+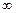 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程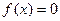 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.(1)求c的值;
(2)求证:
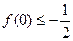 ;
;(3)求|α–β|的取值范围.
(1)0;
(2)证明略;
(3)
(2)证明略;
(3)

(1)解:
由题意知:函数 在(0,+
在(0,+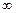 )上是增函数,在[–1,0]上是减函数,
)上是增函数,在[–1,0]上是减函数,
函数 在x=0处有极小值,
在x=0处有极小值,
∴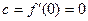
(2)证明:∵ 在(0,+
在(0,+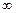 )上是增函数,在[–1,0]上是减函数,
)上是增函数,在[–1,0]上是减函数,
∴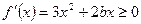 在(0,+
在(0,+ )上恒成立,
)上恒成立,
且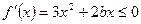 在
在 上恒成立,
上恒成立,
即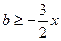 在(0,+
在(0,+ )上恒成立, 在
)上恒成立, 在 上也恒成立,
上也恒成立,
∴b≥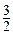 .
.
又∵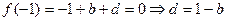 ,
,
∴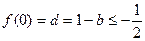 即
即 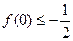 .
.
(3)解:∵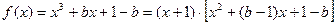 ,
,
∴α,β是方程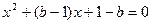 的两根,
的两根,
∴当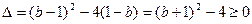

又b≥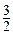 , 所以
, 所以  .
.

由题意知:函数
 在(0,+
在(0,+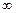 )上是增函数,在[–1,0]上是减函数,
)上是增函数,在[–1,0]上是减函数,函数
 在x=0处有极小值,
在x=0处有极小值,∴
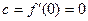
(2)证明:∵
 在(0,+
在(0,+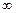 )上是增函数,在[–1,0]上是减函数,
)上是增函数,在[–1,0]上是减函数,∴
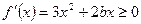 在(0,+
在(0,+ )上恒成立,
)上恒成立,且
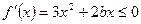 在
在 上恒成立,
上恒成立,即
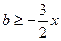 在(0,+
在(0,+ )上恒成立, 在
)上恒成立, 在 上也恒成立,
上也恒成立,∴b≥
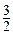 .
.又∵
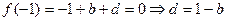 ,
,∴
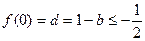 即
即 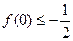 .
.(3)解:∵
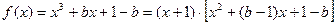 ,
,∴α,β是方程
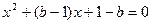 的两根,
的两根,∴当
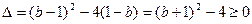

又b≥
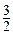 , 所以
, 所以  .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

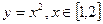 与函数
与函数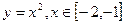 即为“同族函数”,请你找出下面哪个函数解析式也能够被用来构造“同族函数”的是( )
即为“同族函数”,请你找出下面哪个函数解析式也能够被用来构造“同族函数”的是( )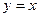
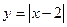
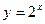
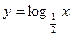
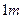 的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记
的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是
,则S的最小值是 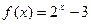 零点所在的区间是 ( )
零点所在的区间是 ( )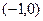
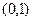
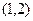
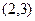
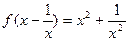 ,则
,则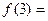 ( )
( ) 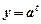 (t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于
(t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于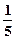 ;②每月减少的有害物质量都相等;③若剩留量为
;②每月减少的有害物质量都相等;③若剩留量为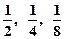 所经过的时间分别是
所经过的时间分别是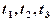 ,则
,则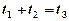 . 其中所有正确的叙述是
. 其中所有正确的叙述是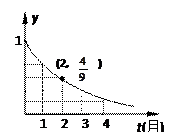
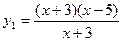 ,
,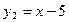 ;
;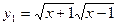 ,
,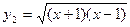 ;
;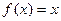 ,
,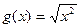 ;
;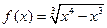 ,
,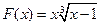 ;
;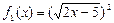 ,
,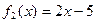 。
。