题目内容

3．边长为2的正方形ABCD，对角线的交点为E，则$（\overrightarrow{AB}+\overrightarrow{AD}）•\overrightarrow{AE}$=4．

分析 由题意可得AE=$\frac{1}{2}$AC=$\sqrt{2}$，$\overrightarrow{AB}$+$\overrightarrow{AD}$=2$\overrightarrow{AE}$，从而求得 $（\overrightarrow{AB}+\overrightarrow{AD}）•\overrightarrow{AE}$=2•${\overrightarrow{AE}}^{2}$ 的值．

解答 解：边长为2的正方形ABCD，对角线的交点为E，可得AE=$\frac{1}{2}$AC=$\sqrt{2}$．
又$\overrightarrow{AB}$+$\overrightarrow{AD}$=2$\overrightarrow{AE}$，∴$（\overrightarrow{AB}+\overrightarrow{AD}）•\overrightarrow{AE}$=2$\overrightarrow{AE}$•$\overrightarrow{AE}$=2•${\overrightarrow{AE}}^{2}$=4，
故答案为：4．

点评 本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，属于基础题．

练习册系列答案
相关题目
13．设a=sin42°，b=cos46°，c=2${\;}^{-\frac{1}{2}}$，则（　　）
A．c＜a＜bB．b＜c＜aC．a＜b＜cD．b＜a＜c
14．已知等比数列{an}的公比q＞1，前n项和为Sn，S3=7，且a1+3，3a2，a3+4成等差数列，数列{bn}满足关系式bn（3n-5）=bn-1（3n-2）其中n≥2，n∈N+，且b1=1．
（1）求数列{an}及{bn}的通项公式；
（2）设A={a1，a2，…a10}，B={b1，b2，…b50}，C=A∪B，求集合C中所有元素之和．
11．已知m，n是平面α外的两条不同的直线．若m，n在平面α内的射影分别是两条直线m′和n′，则“m⊥n”是“m′⊥n′”的（　　）
A．充分但不必要条件B．必要但不充分条件
C．充要条件D．既不充分也不必要条件
18．执行下面的程序框图，那么输出的S等于（　　）
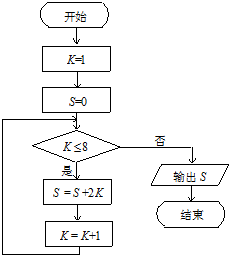
A．42B．56C．72D．90
8．如图，在平面四边形ABCD中，AD=1，CD=2，AC=$\sqrt{7}$，则cos∠CAD=$\frac{2\sqrt{7}}{7}$；又若cos∠BAD=-$\frac{\sqrt{7}}{14}$，sin∠CBA=$\frac{\sqrt{21}}{6}$，则BC=3．
15．设点A、B的坐标分别为（-2，0），（2，0），点P是曲线C上任意一点，且直线PA与PB的斜率之积为$-\frac{1}{4}$，（Ⅰ）求曲线C的方程；
（Ⅱ）过点（m，0）作圆x2+y2=1的切线交曲线C于E、F两点，当|m|＞1时求|EF|的最大值．
12．设a=log3$\sqrt{3}$，b=ln2，c=5${\;}^{-\frac{1}{2}}$，则（　　）
A．c＞b＞aB．b＞a＞cC．a＞c＞bD．a＞b＞c
14．已知{an}为等比数列，a4+a7=2，a5a6=-8，则a1+a10=-7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网