题目内容
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】解:(Ⅰ)根据表中数据,计算随机变量
K2= 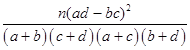 =
= ![]() ≈6.667>6.635,
≈6.667>6.635,
所以能有99%的把握认为是否喜欢读纸质书籍与性别有关系;
(Ⅱ)ξ的可能取值为0、1、2,则P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ;
;
所以ξ的分布列为
ξ | 0 | 1 | 2 |
P |
|
|
|
所以ξ的数学期望为Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =
= ![]()
【解析】(Ⅰ)根据表中数据,计算K2的值,对照数表即可得出结论;(Ⅱ)ξ的可能取值为0、1、2,计算对应的概率值,填写ξ的分布列,计算数学期望值.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目

