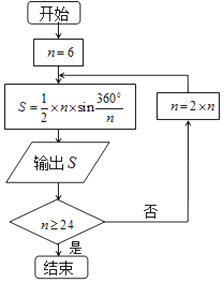
��Ŀ����
����Ŀ����ͼ��P��x0 �� y0������Բ ![]() +y2=1���ϵĵ㣬l����Բ�ڵ�P�������ߣ�O������ԭ�㣬OQ��l����Բ��һ��������Q��P��Q����x���Ϸ�
+y2=1���ϵĵ㣬l����Բ�ڵ�P�������ߣ�O������ԭ�㣬OQ��l����Բ��һ��������Q��P��Q����x���Ϸ�
��1����P�������� ![]() ��
�� ![]() ��ʱ�����������д��l�ķ��̣�����֤lȷ������Բ�����ߣ�
��ʱ�����������д��l�ķ��̣�����֤lȷ������Բ�����ߣ�
��2������P�ڵ�һ�����˶�ʱ������ֱ��Ӧ�ö�����
�����OPQ�����
����ֱ��PQ��y���ϵĽؾ��ȡֵ��Χ��
���������㣨x0 �� y0������Բ ![]() +y2=1�ϣ�����Բ�ڸõ㴦�����߷���Ϊ
+y2=1�ϣ�����Բ�ڸõ㴦�����߷���Ϊ ![]() +y0y=1��
+y0y=1��
���𰸡�
��1���⣺�ɵ㣨x0��y0������Բ ![]() +y2=1�ϣ�����Բ�ڸõ㴦�����߷���Ϊ
+y2=1�ϣ�����Բ�ڸõ㴦�����߷���Ϊ ![]() +y0y=1��
+y0y=1��
��P�� ![]() ��
�� ![]() ������
������ ![]() �������ã�ֱ��l��x+y=2��
�������ã�ֱ��l��x+y=2��
�� 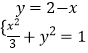 �������ã�4x2��12x+9=0��
�������ã�4x2��12x+9=0��
��=��12��2��4��4��9=0��
��ֱ��l��x+y=2����Բ������
��2���⣺����P��x0��y0������x02+3y02=1��������l�� ![]() +y0y=1��
+y0y=1��
��OQ��x0x+3y0y=0�� ![]() ����ã�
����ã� 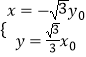 ��
�� 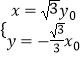
��Q��x���Ϸ�����Q���� ![]() y0��
y0�� ![]() x0����
x0����
��حOQح= ![]() =
= ![]() ��
��
��l��ֱ��OQ֮��ľ���d= ![]() ��
��
�ɡ�OPQ�����S= ![]() ��حOQح��d=
��حOQح��d= ![]() ��
��
����ֱ��PQ��y���M��0��m������P��x0��y0����Q���� ![]() y0��
y0�� ![]() x0����x0x+3y0y=0��
x0����x0x+3y0y=0��
��kPQ=kPM���� ![]() =
= ![]() ��
��
��m=y0�� ![]() =
= ![]() ��
��
3=x02+3y02����x0+ ![]() y0��2��2��x02+3y02��=6��
y0��2��2��x02+3y02��=6��
��m= ![]() ��[
��[ ![]() ��1��
��1��
����������1���ɶ���������߷��̣�������Բ���̣��ɡ�=0����ֱ��l��x+y=2����P�����Բ�����ߣ���2�����ɶ������P������߷��̣��������OQ�ķ��̣�������Բ���̣��������Q�����꣬�������حOQح����l��ֱ��OQ֮��ľ���d��������á�OPQ�����������kPQ=kPM���������m����3=x02+3y02����x0+ ![]() y0��2��2��x02+3y02��=6���������m��ȡֵ��Χ��
y0��2��2��x02+3y02��=6���������m��ȡֵ��Χ��

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�����Ŀ��4��23������������գ�Ϊ���ѧ���Զ�������ӣ��ø�����˳������麣�У��Ӷ��ջ�����֪ʶ��ij���е�Уѧ���Ὺչ������Ϊ�����Ķ���Ϊϰ�ߣ���˼��������������ʵ�����Уѧ����ʵ������ͬѧ�漴�����ѧУ��40����һѧ����ͨ������������ϲ����ֽ���黹��ϲ���������飬���˽���У��һѧ���Ķ���ϰ�ߣ��õ������������
ϲ����ֽ���� | ��ϲ����ֽ���� | �ϼ� | |
�� | 16 | 4 | 20 |
Ů | 8 | 12 | 20 |
�ϼ� | 24 | 16 | 40 |
������������ܷ���99%�İ�����Ϊ�Ƿ�ϲ����ֽ���鼮���Ա��й�ϵ��
���ӱ�����16����ϲ����ֽ���鼮��ѧ���������ȡ2��ѧ������鵽���������εķֲ��м�����ѧ����E���Σ���
�ο���ʽ��K2= ![]() ������n=a+b+c+d��
������n=a+b+c+d��
���е��ٽ�ֵ�����ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |