题目内容
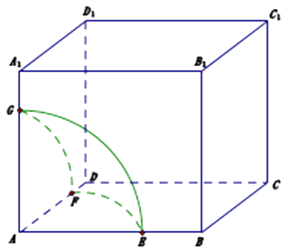
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=1,二面角C﹣AB﹣D的平面角的正切值为 ![]() ,求二面角B﹣AD﹣E的余弦值.
,求二面角B﹣AD﹣E的余弦值.
【答案】(Ⅰ)解:因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又BD⊥DC,所以DC⊥平面ABD.
因为AB平面ABD,所以DC⊥AB.
又因为折叠前后均有AD⊥AB,DC∩AD=D,
所以AB⊥平面ADC
(Ⅱ)由(Ⅰ)知AB⊥平面ADC,所以二面角C﹣AB﹣D的平面角为∠CAD.
又DC⊥平面ABD,AD平面ABD,所以DC⊥AD.
依题意 ![]() .
.
因为AD=1,所以 ![]() .
.
设AB=x(x>0),则 ![]() .
.
依题意△ABD~△BDC,所以 ![]() ,即
,即  .
.
解得 ![]() ,故
,故 ![]() .
.
如图所示,建立空间直角坐标系D﹣xyz,
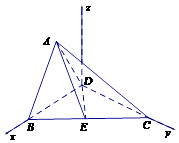
则D(0,0,0), ![]() ,
, ![]() ,
,
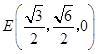 ,
, 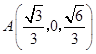 ,
,
所以 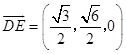 ,
, 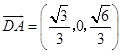 .
.
由(Ⅰ)知平面BAD的法向量 ![]() .
.
设平面ADE的法向量 ![]()
由 ![]() 得
得 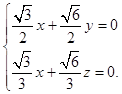
令 ![]() ,得
,得 ![]() ,
,
所以 ![]() .
.
所以 ![]() .
.
由图可知二面角B﹣AD﹣E的平面角为锐角,
所以二面角B﹣AD﹣E的余弦值为 ![]() .
.
【解析】(Ⅰ)证明DC⊥AB.AD⊥AB即可得AB⊥平面ADC.(Ⅱ)由(Ⅰ)知AB⊥平面ADC,即二面角C﹣AB﹣D的平面角为∠CAD二面角C﹣AB﹣D的平面角的正切值为 ![]() ,解得AB,如图所示,建立空间直角坐标系D﹣xyz,求出平面BAD的法向量
,解得AB,如图所示,建立空间直角坐标系D﹣xyz,求出平面BAD的法向量 ![]() ,平面ADE的法向量,即可得二面角B﹣AD﹣E的余弦值
,平面ADE的法向量,即可得二面角B﹣AD﹣E的余弦值
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |