题目内容
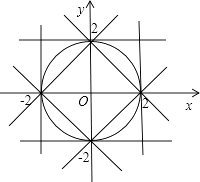
【题目】直线mx+ny=1与圆x2+y2=4的交点为整点(横纵坐标均为正数的点),这样的直线的条数是( )
A.2
B.4
C.6
D.8
【答案】D
【解析】解:由圆的方程x2+y2=4,得到圆心坐标为(0,0),半径r=2,
而圆x2+y2=4上的“整点”有四个,分别是:(0,2),(0,﹣2),(﹣2,0),(2,0),
如图所示:
根据图形得到mx+ny=1可以为:
直线y=2,y=﹣2,x=2,x=﹣2,x+y=2,x+y=﹣2,x﹣y=2,x﹣y=﹣2,共8条,
则这样的直线的条数是8条.
故选:D.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.

【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 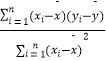 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.