题目内容
3．设等差数列{an}与{bn}的前n项和分别为Sn和Tn，并且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n+2}{3n+4}$对于一切n都成立，则$\frac{{a}_{12}}{{b}_{12}}$=$\frac{25}{73}$．分析 由等差数列的求和公式和性质可得$\frac{{a}_{12}}{{b}_{12}}$=$\frac{{S}_{23}}{{T}_{23}}$，代值计算可得．
解答 解：由等差数列的求和公式和性质可得：
$\frac{{a}_{12}}{{b}_{12}}$=$\frac{2{a}_{12}}{2{b}_{12}}$=$\frac{{a}_{1}+{a}_{23}}{{b}_{1}+{b}_{23}}$=$\frac{\frac{23（{a}_{1}+{a}_{23}）}{2}}{\frac{23（{b}_{1}+{b}_{23}）}{2}}$
=$\frac{{S}_{23}}{{T}_{23}}$=$\frac{23+2}{3×23+4}$=$\frac{25}{73}$
故答案为：$\frac{25}{73}$．
点评 本题考查等比数列的性质和求和公式，属基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
14．从一副不含大、小王的52张扑克牌中任意抽出5张，则至少有3张是A的概率为（ ）
| A． | $\frac{{{C}_{4}^{3}C}_{48}^{2}}{{C}_{52}^{5}}$ | B． | $\frac{{{C}_{48}^{3}C}_{4}^{2}}{{C}_{52}^{5}}$ | ||
| C． | 1-$\frac{{{C}_{48}^{1}C}_{4}^{4}}{{C}_{52}^{5}}$ | D． | $\frac{{{C}_{4}^{3}C}_{48}^{2}{{+C}_{4}^{4}C}_{48}^{1}}{{C}_{52}^{5}}$ |
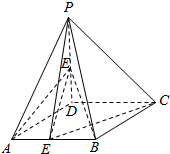如图所示，已知正四棱锥P-ABCD的所有棱长都为1，且E、F分别为AB，PD的中点．