题目内容
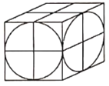
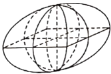
【题目】魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”(如图所示),刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为![]() .若“牟合方盖”的体积为
.若“牟合方盖”的体积为![]() ,则正方体的外接球的表面积为__________.
,则正方体的外接球的表面积为__________.
【答案】![]()
【解析】
根据已知求出正方体的内切球的体积,得到内切球的半径,根据正方体内切球的直径为其棱长,外接球的直径为其对角线,即可求解.
因为“牟合方盖”的体积为![]() ,
,
又正方体的内切球的体积与“牟合方盖”的体积之比应为![]() ,
,
所以正方体的内切球的体积![]() 球
球![]() ,
,
所以内切球的半径![]() ,所以正方体的棱长为2,
,所以正方体的棱长为2,
所以正方体的外接球的直径等于正方体的体对角线即![]() ,
,
所以![]() ,所以正方体的外接球的表面积为
,所以正方体的外接球的表面积为![]() .
.
故答案为:![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目