题目内容
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
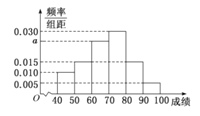
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中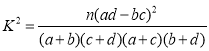 ,
,![]() .
.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)根据概率的性质知所有矩形的面积之和等于![]() 列式可解得;
列式可解得;
(Ⅱ)由频率分布直方图知样本中获奖的人数为![]() ,不获奖的人数为
,不获奖的人数为![]() ,从而可得
,从而可得![]() 列联表,再计算出
列联表,再计算出![]() ,与临界值比较可得.
,与临界值比较可得.
解:(Ⅰ)![]()
![]()
![]() ,
,
![]()
![]() .
.
(Ⅱ)由频率分布直方图知样本中获奖的人数为![]() ,不获奖的人数为
,不获奖的人数为![]() ,
,
![]() 列联表如下:
列联表如下:
女生 | 男生 | 总计 | |
获奖 |
|
|
|
不获奖 |
|
|
|
总计 |
|
|
|
因为![]()
![]() ,
,
所以在犯错误的概率不超过![]() 的前提下能认为“获奖与女生,男生有关.”
的前提下能认为“获奖与女生,男生有关.”

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: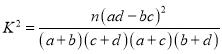
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |