题目内容
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
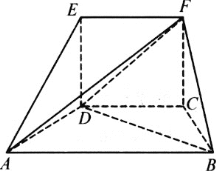
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
【答案】(1)见解析:(2)![]()
【解析】
(1)推导出AD⊥DE,CD⊥DE,从而DE⊥平面ABCD,由此能证明平面ABCD⊥平面EDCF,(2)三棱锥A﹣BDF的体积VA﹣BDF=VF﹣ABD![]() ,由此能求出结果.
,由此能求出结果.
(1)证明:∵在五面体ABCDEF中,四边形EDCF是正方形,∠ADE=90°,
∴AD⊥DE,CD⊥DE,
∵AD∩CD=D,∴DE⊥平面ABCD,
∵DE平面EDCF,∴平面ABCD⊥平面EDCF.
(2) 由(1)知DE⊥平面![]() ,所以
,所以![]() 平面
平面![]() . 等腰三角形
. 等腰三角形![]()
又DC∥EF,![]() 平面ABFE,
平面ABFE,![]() 平面ABFE,所以DC∥平面ABFE.
平面ABFE,所以DC∥平面ABFE.
又平面ABCD∩平面ABFE=AB,故AB∥CD.所以四边形![]() 为等腰梯形.又AD=DE,所以AD=CD=CB,由
为等腰梯形.又AD=DE,所以AD=CD=CB,由![]() ,在等腰
,在等腰![]() 中由余弦定理得BD=
中由余弦定理得BD=![]() ,
,![]() AD
AD![]() BD,所以三棱锥
BD,所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目