题目内容
【题目】为响应绿色出行，某市在推出“共享单车”后，又推出“新能源租赁汽车”．每次租车收费的标准由两部分组成：①里程计费：1元/公里；②时间计费：
元/分．已知陈先生的家离上班公司
公里，每天上、下班租用该款汽车各一次．一次路上开车所用的时间记为
（分），现统计了50次路上开车所用时间，在各时间段内频数分布情况如下表所示
将各时间段发生的频率视为概率，一次路上开车所用的时间视为用车时间，范围为
分．
（1）估计陈先生一次租用新能源租赁汽车所用的时间不低于
分钟的概率；
（2）若公司每月发放
元的交通补助费用，请估计是否足够让陈先生一个月上下班租用新能源租赁汽车（每月按
天计算），并说明理由.（同一时段，用该区间的中点值作代表）
【答案】（1）
；（2）见解析
【解析】分析：（1）利用对立事件的概率公式求陈先生一次租用新能源租赁汽车的时间不低于30分钟的概率.(2)比较每个月的费用和
元的大小，即得解.
详解：（1）设“陈先生一次租用新能源租赁汽车的时间不低于30分钟”的事件为
则所求的概率为
所以陈先生一次租用新能源租赁汽车的时间不低于30分钟的概率为.
（2）每次开车所用的平均时间为
每次租用新能源租赁汽车的平均费用为
每个月的费用为
，
因此公车补贴够上下班租用新能源分时租赁汽车.
阅读快车系列答案【题目】基于移动网络技术的共享单车被称为“新四大发明”之一，短时间内就风靡全国，给人们带来新的出行体验，某共享单车运营公司的市场研究人员为了了解公司的经营状况，对公司最近6个月的市场占有率
进行了统计，结果如下表：
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
（1）请用相关系数说明能否用线性回归模型拟合
与月份代码
之间的关系.如果能，请计算出关于的线性回归方程，如果不能，请说明理由；
（2）根据调研数据，公司决定再采购一批单车扩大市场，从成本1000元/辆的
型车和800元/辆的
型车中选购一种，两款单车使用寿命频数如下表：
| 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算，平均每辆单车每年能为公司带来500元的收入，不考虑除采购成本以外的其它成本，假设每辆单车的使用寿命都是整数年，用频率估计每辆车使用寿命的概率，以平均每辆单车所产生的利润的估计值为决策依据，如果你是公司负责人，会选择哪款车型？
参考数据：
，
，
，
.
参考公式：相关系数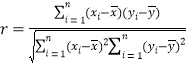
，
，
.
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
