题目内容
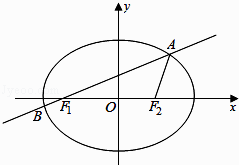
【题目】如图，点A，B分别是椭圆 
的长轴的左右端点，点F为椭圆的右焦点，直线PF的方程为： 
且PA⊥PF．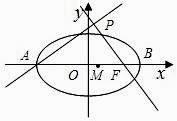 
（1）求直线AP的方程；
（2）设点M是椭圆长轴AB上一点，点M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．
【答案】
（1）解：由题意得 
，A的坐标为（﹣6，0）
则直线AP的方程为： 
．
（2）解：设M（m，0），则 
，解得m=2或m=18（舍去），故M（2，0）．
，x∈[﹣6，6]，
所以当 
时，dmin2=15，即 
【解析】（1）根据两直线垂直，求得AP的斜率，利用椭圆方程求得A的坐标，然后利用点斜式求得直线AP的方程．（2）设出点M的坐标，利用两点间的距离公式利用题设建立等式求得m，进而可利用两点间的距离公式，表示出椭圆上的点到点M的距离d，利用x的范围和二次函数的单调性求得函数的最小值．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据： 
， 
，
如果由资料知y对x呈线性相关关系．试求：
（1）
；
（2）线性回归方程 
=bx+a．
（3）估计使用10年时，维修费用是多少？
