题目内容
已知直线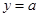 交抛物线
交抛物线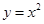 于
于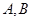 两点.若该抛物线上存在点
两点.若该抛物线上存在点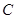 ,使得
,使得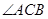 为直角,则
为直角,则 的取值范围为 .
的取值范围为 .
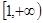
解析试题分析:如图所示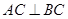 ,则
,则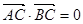 又
又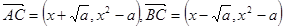 所以
所以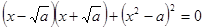 ,即
,即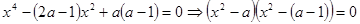 ,因为
,因为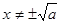 所以
所以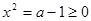 .
.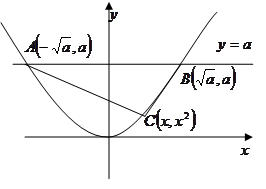
考点:平面向量的数量积、函数与方程的思想.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
题目内容
已知直线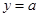 交抛物线
交抛物线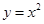 于
于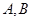 两点.若该抛物线上存在点
两点.若该抛物线上存在点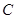 ,使得
,使得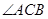 为直角,则
为直角,则 的取值范围为 .
的取值范围为 .
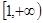
解析试题分析:如图所示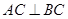 ,则
,则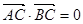 又
又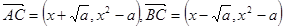 所以
所以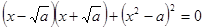 ,即
,即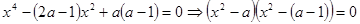 ,因为
,因为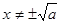 所以
所以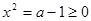 .
.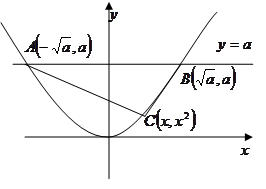
考点:平面向量的数量积、函数与方程的思想.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案