题目内容
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳组的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 | P |
第三组 |
| 100 | 0.5 |
第四组 |
| a | 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
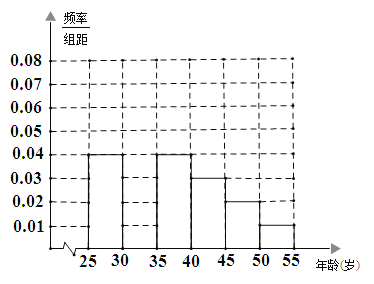
(1)补全频率分布直方图,并求n,a,p的值;
(2)求年龄段人数的中位数和众数;(直接写出结果即可)
(3)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在
岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在![]() 岁的概率.
岁的概率.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)中位数为35,众数为32.5;(3)
;(2)中位数为35,众数为32.5;(3)![]()
【解析】
(1)求出第二组的频率,由频率除以组距可补全频率直方图,由第一组的人数和频率可求得总人数![]() ,由第二组的频率求得第二组的人数,可求得
,由第二组的频率求得第二组的人数,可求得![]() ,由第四组的频率可得出第四组的人数,求得
,由第四组的频率可得出第四组的人数,求得![]() .
.
(2)在频率直方图中从左至右找到频率为0.5的数据可得中位数,频率直方图中最高一组的中间值可得众数;
(3)由频率直方图得出![]() 岁年龄段的“低碳族”与
岁年龄段的“低碳族”与![]() 岁年龄段的“低碳族”的比值,根据分层抽样法得出在
岁年龄段的“低碳族”的比值,根据分层抽样法得出在![]() ,
,![]() 中所抽取的人数,再运用古典概型可求得概率.
中所抽取的人数,再运用古典概型可求得概率.
(1)第二组的频率为![]() ,所以高为
,所以高为![]() ,频率直方图如图:
,频率直方图如图:
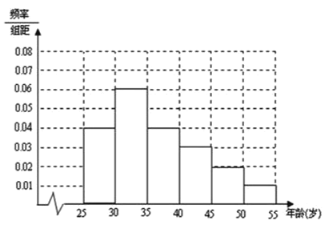
第一组的人数为![]() ,频率为
,频率为![]() ,所以
,所以![]() .
.
由题可知,第二组的频率为0.3,所以第二组的人数为![]() ,所以
,所以![]() ,
,
第四组的频率为![]() ,所以第四组的人数为
,所以第四组的人数为![]() ,所以
,所以![]() .
.
所以,![]() ,
,![]() ,
,![]() ;
;
(2)中位数为35,众数为32.5;
(3)因为![]() 岁年龄段的“低碳族”与
岁年龄段的“低碳族”与![]() 岁年龄段的“低碳族”的比值为
岁年龄段的“低碳族”的比值为![]() ,
,
所以采用分层抽样法抽取6人,![]() 岁中有4人,
岁中有4人,![]() 岁中有2人.由于从6人中选取3人作领队的所有可能情况共20种,其中从
岁中有2人.由于从6人中选取3人作领队的所有可能情况共20种,其中从![]() 岁中的4人中选取3名领队的情况有4种,故所求概率为
岁中的4人中选取3名领队的情况有4种,故所求概率为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: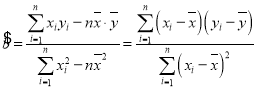 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)


