Question

【题目】已知函数f（x）=|x+ |﹣|x﹣ |；
（1）作出函数f（x）的图象；
（2）根据（1）所得图象，填写下面的表格：

性质	定义域	值域	单调性	奇偶性	零点
f（x）

（3）关于x的方程f2（x）+m|f（x）|+n=0（m，n∈R）恰有6个不同的实数解，求n的取值范围．

Answer 1

【答案】
（1）解：函数f（x）=|x+ |﹣|x﹣ |= ，

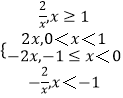作出函数f（x）的图象如图：

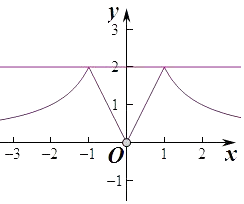
（2）解：由函数的图象得函数的定义域为{x|x≠0}，

函数的值域为（0，2]，

在（﹣∞，﹣1]和（0，1）上单调递增，

在[1，+∞）和（﹣1，0），单调递减，

函数关于y轴对称，是偶函数，

函数与x轴没有交点，无零点

（3）解：∵0＜f（x）≤2，且函数f（x）为偶函数，

∴令t=f（x），则方程等价为t2+mt+n=0，

则由图象可知，当0＜t＜2时，方程t=f（x）有4个不同的根，

当t=2时，方程t=f（x）有2个不同的根，

当t≤0或t＞2时，方程t=f（x）有0个不同的根，

若方程f2（x）+m|f（x）|+n=0（m，n∈R）恰有6个不同的实数解，等价为方程f2（x）+mf（x）+n=0（m，n∈R）恰有6个不同的实数解，

即t2+mt+n=0有两个不同的根，

其中t1=2，0＜t2＜2，

则n=t1t2∈（0，4）．

【解析】（1）利用分段函数求出f（x）的表达式，然后作出函数f（x）的图象，（2）结合函数的图象判断相应的性质，（3）根据图象利用换元法将条件进行转化，利用数形结合即可得到结论．