题目内容
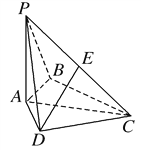
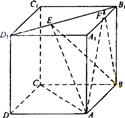
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?

【答案】(1)![]() (2)当材料长为
(2)当材料长为 ![]() ,宽为
,宽为 ![]() 时,S2最大.(3)当材料长为
时,S2最大.(3)当材料长为 ![]() ,宽为
,宽为 ![]() 时,S1+2S2最大
时,S1+2S2最大
【解析】
试题分析:(1)设![]() 米,通过三角形全等以及勾股定,即可用
米,通过三角形全等以及勾股定,即可用![]() 表示图中
表示图中![]() 的长度,并写出
的长度,并写出![]() 的取值范围;
的取值范围;
(2)表示面积![]() ,利用基本不等式求解最大值,即可求得材料的长和宽的值;
,利用基本不等式求解最大值,即可求得材料的长和宽的值;
(3)表示面积![]() 的表达式,利用导数求解函数的最值即可.
的表达式,利用导数求解函数的最值即可.
试题分析:
解:(Ⅰ)由题意,AB=x,BC=2﹣x,∵x>2﹣x,∴1<x<2
设DP=y,则PC=x﹣y,由△ADP≌△CB'P,故PA=PC=x﹣y,
由PA2=AD2+DP2,得(x﹣y)2=(2﹣x)2+y2
即: ![]() .
.
(Ⅱ)记△ADP的面积为S2,则 ![]() .
.
当且仅当 ![]() 时,S2取得最大值.
时,S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S2最大.
时,S2最大.
(Ⅲ) ![]()
于是令 ![]() ,∴
,∴ ![]()
∴关于x的函数 ![]() 在
在 ![]() 上递增,在
上递增,在 ![]() 上递减,
上递减,
∴当 ![]() 时,S1+2S2取得最大值.
时,S1+2S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S1+2S2最大
时,S1+2S2最大

 名校课堂系列答案
名校课堂系列答案【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2= ![]() [
[ ![]() +
+ ![]() +…+
+…+ ![]() ],其中
],其中 ![]() 为数据x1 , x2 , …,xn的平均数)
为数据x1 , x2 , …,xn的平均数)