题目内容
一条直线和一个平面所成的角为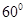 ,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
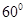 ,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
本试题主要是考查了线线角的求解问题的运用。根据已知条件可知,线面角是直线和平面内所有直线中所成角中最小的角,而平面内不经过斜足的所有直线,即异面直线的时候,会出现垂直时最大,且是异面垂直。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
题目内容
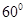 ,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案