题目内容
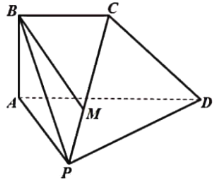
【题目】在四棱锥![]() 中,
中,![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,E为
,E为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
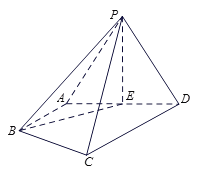
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点M,使得
上是否存在点M,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)在棱
;(Ⅲ)在棱![]() 上存在点M满足题意,
上存在点M满足题意,![]() .
.
【解析】
(Ⅰ)根据面面垂直的性质定理可证得![]() 平面
平面![]() ,由面面垂直的判定定理证得结论;
,由面面垂直的判定定理证得结论;
(Ⅱ)取![]() 中点
中点![]() ,可证得
,可证得![]() 两两互相垂直,由此以
两两互相垂直,由此以![]() 为坐标原点建立空间直角坐标系,根据线面角的向量求法可求得结果;
为坐标原点建立空间直角坐标系,根据线面角的向量求法可求得结果;
(Ⅲ)假设存在点![]() 满足题意,由线面垂直的性质可知
满足题意,由线面垂直的性质可知![]() ,
,![]() ,由此得到
,由此得到 ,解出
,解出![]() 后即可得到结果.
后即可得到结果.
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
![]() 分别为
分别为![]() 中点,
中点,![]() ,
,![]() 平面
平面![]() ;
;
![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
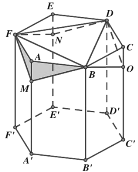
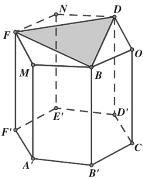
则以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,可建立如下图所示空间直角坐标系,
轴,可建立如下图所示空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
, .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)假设在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
 ,解得:
,解得:![]() ,即
,即![]() ,
,
![]() 在棱
在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() .
.

【题目】![]() 大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查,经统计发现,他们的月薪收入在3000元到10000元之间,具体统计数据如表:
大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查,经统计发现,他们的月薪收入在3000元到10000元之间,具体统计数据如表:
月薪(百万) |
|
|
|
|
|
|
|
人数 | 2 | 15 | 20 | 15 | 24 | 10 | 4 |
(1)经统计发现,该大学2018届的大学本科毕业生月薪![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).若
(每组数据取区间的中点值).若![]() 落在区间
落在区间![]() 的左侧,则可认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,为以后的毕业生就业提供更好的指导意见.现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生;
的左侧,则可认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,为以后的毕业生就业提供更好的指导意见.现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生;
(2)①将样本的频率视为总体的概率,若![]() 大学领导决定从
大学领导决定从![]() 大学2018届所有本毕业生中任意选取5人前去探访,记这5人中月薪不低于8000元的人数为
大学2018届所有本毕业生中任意选取5人前去探访,记这5人中月薪不低于8000元的人数为![]() ,求
,求![]() 的数学期望与方差;
的数学期望与方差;
②在(1)的条件下,中国移动赞助了![]() 大学的这次社会调查活动,并为这次参与调查的大学本科毕业生制定了赠送话费的活动,赠送方式为:月薪低于
大学的这次社会调查活动,并为这次参与调查的大学本科毕业生制定了赠送话费的活动,赠送方式为:月薪低于![]() 的获赠两次随机话费,月薪不低于
的获赠两次随机话费,月薪不低于![]() 的获赠一次随机话费;每次赠送的话费及对应的概率分别为:
的获赠一次随机话费;每次赠送的话费及对应的概率分别为:
赠送话费(单位:元) | 50 | 100 | 150 |
概率 |
|
|
|
则张茗预期获得的话费为多少元?(结果保留整数)