题目内容
【题目】已知函数 
，
（1）求f（x）的定义域；
（2）求使f（x）＞0的x的取值范围．
【答案】
（1）解：求函数 
的定义域，
即： 
．
所以，定义域是（﹣1，1）
（2）解： 
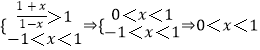
所以x的取值范围为0＜x＜1
【解析】首先对于（1）分析对数函数 ，所以定义域应为 
，解出即可得到答案．对于（2）f（x）＞0，列出式子 
，且要满足x属于定义域，解不等式即可．
【考点精析】通过灵活运用函数单调性的判断方法和对数函数的单调性与特殊点，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数即可以解答此题．
练习册系列答案
相关题目
