题目内容
【题目】设f（x）=（log2x）2﹣2alog2x+b（x＞0）．当x= 
时，f（x）有最小值﹣1．
（1）求a与b的值；
（2）求满足f（x）＜0的x的取值范围．
【答案】
（1）
解：f（x）=（log2x）2﹣2alog2x+b= 
+b﹣a2（x＞0），
当x= 
时，f（x）有最小值﹣1，
∴ 
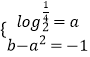，解得： 
（2）
解：由（1）得：f（x）=（log2x）2+4log2x+3，
f（x）＜0即（log2x+3）（log2x+1）＜0，
解得： 
＜x＜ 
【解析】（1）利用配方法，结合x= 时，f（x）有最小值﹣1，建立方程组，即可求a与b的值；（2）f（x）＜0即（log2x）2+4log2x+3＜0，即可求出x的范围．
练习册系列答案
阅读快车系列答案
相关题目
