题目内容
(10分)选修4-1:几何证明选讲.
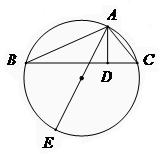
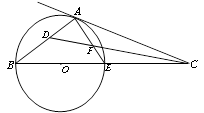
已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是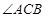 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.
(1) 求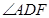 的度数;
的度数;
(2) 若AB=AC,求AC:BC.
已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是
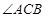 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.
(1) 求
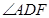 的度数;
的度数;(2) 若AB=AC,求AC:BC.
(1) ;(2)
;(2) 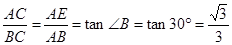
 ;(2)
;(2) 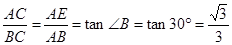
本题考查的知识点是圆周角定理,三角形外角定理,弦切角定理,相似三角形的证明及性质等,本题中未给出任何角的度数,故建立∠ADF必为特殊角,从而根据图形分析角∠ADF的大小,进而寻出解答思路是解题的关键.
(I)根据AC为圆O的切线,结合弦切角定理,我们易得∠B=∠EAC,结合DC是∠ACB的平分线,根据三角形外角等于不相邻两个内角的和,我们易得∠ADF=∠AFD,进而结合直径所对的圆周角为直角,求出∠ADF的度数;
(II)若AB=AC,结合(1)的结论,我们易得∠ACB=30°,根据顶角为120°的等腰三角形三边之比为:1:1: 3,易得答案.
解: AC为圆O的切线,∴
AC为圆O的切线,∴ 又知,DC是
又知,DC是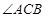 的平分线,
的平分线,
∴ ∴
∴
即 又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴
∴
(2)
 ,
, ,∴
,∴ ∽
∽ ∴
∴
又 AB="AC," ∴
AB="AC," ∴ ,
,
∴在Rt⊿ABE中,
(I)根据AC为圆O的切线,结合弦切角定理,我们易得∠B=∠EAC,结合DC是∠ACB的平分线,根据三角形外角等于不相邻两个内角的和,我们易得∠ADF=∠AFD,进而结合直径所对的圆周角为直角,求出∠ADF的度数;
(II)若AB=AC,结合(1)的结论,我们易得∠ACB=30°,根据顶角为120°的等腰三角形三边之比为:1:1: 3,易得答案.
解:
 AC为圆O的切线,∴
AC为圆O的切线,∴ 又知,DC是
又知,DC是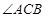 的平分线,
的平分线,∴
 ∴
∴
即
 又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴
∴

(2)

 ,
, ,∴
,∴ ∽
∽ ∴
∴
又
 AB="AC," ∴
AB="AC," ∴ ,
,∴在Rt⊿ABE中,


练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
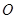 的半径OB垂直于直径AC,
的半径OB垂直于直径AC,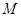 为AO上一点,
为AO上一点, 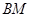 的延长线交⊙
的延长线交⊙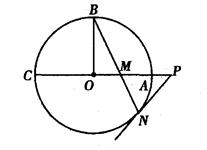
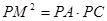 ;
;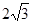 ,OA=
,OA=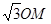 ,求
,求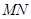 的长.
的长.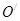 相交于
相交于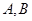 两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E。证明
两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E。证明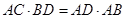 ;
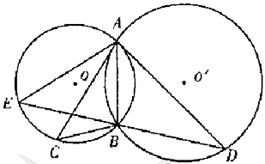
;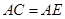 。
。
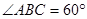 ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
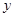 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.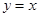 的交点为N.设
的交点为N.设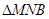 的周长为
的周长为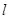 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中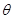 ,当
,当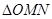 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.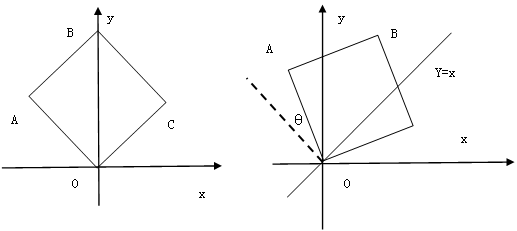

 与曲线
与曲线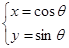
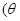 为参数,且
为参数,且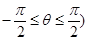 有两个不同的交点,则实数
有两个不同的交点,则实数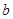 的取值范围是__________.
的取值范围是__________.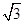 ,PC=1,则圆O的半径为________ .
,PC=1,则圆O的半径为________ .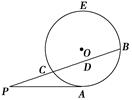
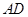 是
是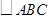 的高,
的高,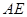 是
是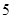 ,
,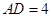 ,
,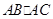 的值。
的值。