题目内容
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD, 
(Ⅰ)求证:平面PED⊥平面PAC;
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
【答案】解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA ∴PA⊥平面ABCD
结合AB⊥AD,可得
分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示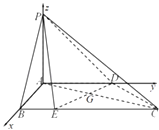
可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),
P(0,0,λ) (λ>0)
∴ ![]() ,
, ![]() ,
, ![]()
得 ![]() ,
, ![]() ,
,
∴DE⊥AC且DE⊥AP,
∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.
∵ED平面PED∴平面PED⊥平面PAC
(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是 ![]() ,
,![]()
设直线PE与平面PAC所成的角为θ,
则 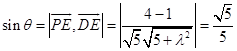 ,解之得λ=±2
,解之得λ=±2
∵λ>0,∴λ=2,可得P的坐标为(0,0,2)
设平面PCD的一个法向量为 ![]() =(x0 , y0 , z0),
=(x0 , y0 , z0), ![]() ,
, ![]()
由 ![]() ,
, ![]() ,得到
,得到 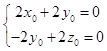 ,
,
令x0=1,可得y0=z0=﹣1,得 ![]() =(1,﹣1,﹣1)
=(1,﹣1,﹣1)
∴cos< ![]() ,
, ![]()
由图形可得二面角A﹣PC﹣D的平面角是锐角,
∴二面角A﹣PC﹣D的平面角的余弦值为 ![]() .
.
【解析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到 ![]() 、
、 ![]() 、
、 ![]() 的坐标.由数量积的坐标运算公式算出
的坐标.由数量积的坐标运算公式算出 ![]() 且
且 ![]() ,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是
,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是 ![]() ,算出
,算出 ![]() 、
、 ![]() 夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出
夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出 ![]() =(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量
=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量 ![]() ,算出
,算出 ![]() 、
、 ![]() 的夹角余弦,再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值.
的夹角余弦,再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案