题目内容
20.执行如图所示的程序框图后,输出的值为5,则P的取值范围是$\frac{7}{8}<p≤\frac{15}{16}$
分析 模拟执行程序框图,依次写出每次循环得到的S,n的值,当S=$\frac{7}{8}$时由题意此时不满足条件$\frac{7}{8}$<P,退出循环,输出n的值为4,从而可解得p的取值范围.
解答 解:模拟执行程序框图,可得
n=1,S=0
满足条件S<P,S=$\frac{1}{2}$,n=2
满足条件S<P,S=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$,n=3
满足条件S<P,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=$\frac{7}{8}$,n=4
满足条件S<P,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$=$\frac{15}{16}$,n=5
由题意可得,此时,不满足条件$\frac{15}{16}$<P,退出循环,输出n的值为5,
既有:$\frac{15}{16}$≥P>$\frac{7}{8}$,
故答案为:$\frac{7}{8}<p≤\frac{15}{16}$.
点评 本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的S,n的值是解题的关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.某程序的框图如图所示,输入N=5,则输出的数等于( )


| A. | $\frac{5}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{5}$ | D. | $\frac{4}{5}$ |
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点是Fl,P是双曲线右支上的点,若线段PF1与y轴的交点M恰好为PF1的中点,且|OM|=a,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
5.如图的程序是用来计算( )


| A. | 3×10的值 | B. | 1×2×3×…×10的值 | C. | 39的值 | D. | 310的值 |
9.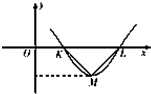 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
 如图,P是圆O外一点,PA、PB是圆O的两条切线,切点分别为A、B,PA的中点为M,过M作圆O的一条割线交圆O于C、D两点,若PB=2$\sqrt{3}$,MC=1,则CD=2.
如图,P是圆O外一点,PA、PB是圆O的两条切线,切点分别为A、B,PA的中点为M,过M作圆O的一条割线交圆O于C、D两点,若PB=2$\sqrt{3}$,MC=1,则CD=2.