题目内容
【题目】正方体ABCD-A1B1C1D1中,BB1与平面ACD1所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
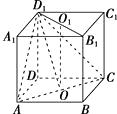
【解析】解法一:如图,设正方体的棱长为 ![]() ,上,下底面的中心分别为
,上,下底面的中心分别为 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() 与平面ACD1所成的角就是BB1与平面ACD1所成的角,即∠O1OD1 , cos∠O1OD1=
与平面ACD1所成的角就是BB1与平面ACD1所成的角,即∠O1OD1 , cos∠O1OD1= ![]() .
.
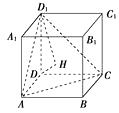
解法二:画出图形,如图,BB1与平面ACD1所成的角等于DD1与平面ACD1所成的角,在三棱锥D-ACD1中,由三条侧棱两两垂直且相等得点D在底面ACD1内的射影为等边三角形ACD1的重心,即中心H,连接D1H,DH,则∠DD1H为DD1与平面ACD1所成的角,设正方体的棱长为a,则cos∠DD1H= ![]() .
.
故答案为:D.
由正方体的结构特征,找到BB1在平面平面 AC D 1 内的射影为OD1,于是 ∠O1OD1就是所求的角,在对应三角形中求解。

练习册系列答案
相关题目






