Question

【题目】已知函数f（x）=alnx﹣ x2+bx存在极小值，且对于b的所有可能取值，f（x）的极小值恒大于0，则a的最小值为 ．

Answer 1

【答案】﹣e3
【解析】解：函数的定义域为（0，+∞），

则函数的导数f′（x）= ﹣x+b，

若函数f（x）=alnx﹣ x2+bx存在极小值，

则f′（x）= ﹣x+b=0有解，

即﹣x2+bx+a=0有两个不等的正根，

则 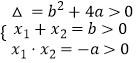，得b＞2 ，（a＜0），

由f′（x）=0得x1= ，x2= ，

分析易得f（x）的极小值点为x1，

∵b＞2 ，（a＜0），

∴x1= = ∈（0， ），

则f（x）极小值=f（x1）=alnx1﹣ x12+bx1=alnx1﹣ x12+x12﹣a=alnx1+ x12﹣a，

设g（x）=alnx+ x2﹣a，x∈（0， ），

f（x）的极小值恒大于0等价为g（x）恒大于0，

∵g′（x）= +x= ＜0，

∴g（x）在（0， ）上单调递减，

故g（x）＞g（ ）=aln ﹣ a≥0，

得ln ≤ ，即﹣a≤e3，则a≥﹣e3，

故a的最小值为是﹣e3，

所以答案是：﹣e3．

【考点精析】本题主要考查了函数的极值与导数的相关知识点，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．