题目内容
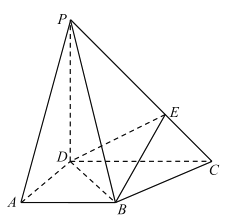
【题目】在底面是边长为6的正方形的四棱锥P--ABCD中,点P在底面的射影H为正方形ABCD的中心,异面直线PB与AD所成角的正切值为![]() ,则四棱锥P--ABCD的内切球与外接球的半径之比为( )
,则四棱锥P--ABCD的内切球与外接球的半径之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
确定异面直线PB与AD所成角为∠PBC,取BC中点E,则tan∠PBC![]() ,求出PE=5,HP=4,可得四棱锥P﹣ABCD的表面积、体积,进而求出内切球的半径,利用勾股定理求出外接球的半径,即可求出四棱锥P﹣ABCD的内切球与外接球的半径之比.
,求出PE=5,HP=4,可得四棱锥P﹣ABCD的表面积、体积,进而求出内切球的半径,利用勾股定理求出外接球的半径,即可求出四棱锥P﹣ABCD的内切球与外接球的半径之比.
由题意,四棱锥P﹣ABCD为正四棱锥,PA=PB=PC=PD,
∵AD∥BC,
∴异面直线PB与AD所成角为∠PBC,
取BC中点E,则tan∠PBC![]() ,
,
∴PE=5,HP=4,
从而四棱锥P﹣ABCD的表面积为S![]() 96,V
96,V![]() 48,
48,
∴内切球的半径为r![]() .
.
设四棱锥P﹣ABCD外接球的球心为O,外接球的半径为R,则OP=OA,
∴(4﹣R)2+(3![]() )2=R2,
)2=R2,
∴R![]() ,
,
∴![]() .
.
故选D.

练习册系列答案
相关题目