题目内容
【题目】如图,四面体ABCD中,O是BD中点,AB=AD=2,![]() .
.

(1)求证:AO⊥平面BCD;
(2)求点D到平面ABC的距离。
【答案】(1)详见解析(2)![]()
【解析】
(1)利用等腰三角形和勾股定理得到AO与BD,OC垂直,即可得证;
(2)利用第一步得到的三线垂直,建立空间坐标系,容易找到各点坐标,从而得到所需向量和法向量,代入公式即可得解.
(1)连接OC,
∵BO=DO,AB=AD,
∴AO⊥BD,
∵BO=DO,BC=CD,
∴CO⊥BD,
在△AOC中,由题设知
AO![]() ,
,![]() ,AC
,AC![]() ,
,
∴AO2+CO2=AC2,
∴∠AOC=90°,
即AO⊥OC,
∵BD∩OC=O,
∴AO⊥平面BCD;
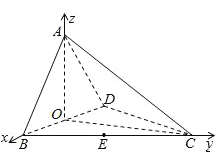
(2)以O为原点,如图建立空间直角坐标系,
则A(0,0,![]() ),B(
),B(![]() ,0,0),
,0,0),
C(0,![]() ,0),D(
,0),D(![]() ,0,0),
,0,0),
![]() ,
,![]() .
.
设平面ABC的一个法向量为![]() (x,y,z),
(x,y,z),
则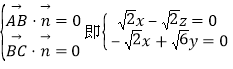
令y=1,得![]() (
(![]() ,1,
,1,![]() )
)
又![]() ,
,
∴点D到平面ABC的距离
 ,
,
即点D到平面ABC的距离为![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目