题目内容
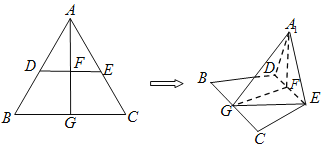
【题目】边长为2的正三角形ABC中，点D，E，G分别是边AB，AC，BC的中点，连接DE，连接AG交DE于点
现将
沿DE折叠至
的位置，使得平面
平面BCED，连接A1G，EG．
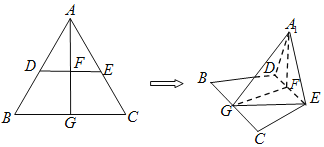
证明：DE∥平面A1BC
求点B到平面A1EG的距离．
【答案】（1）见解析；（2）
【解析】
（1）推导出DE∥BC，由此能证明DE∥平面A1BC．
（2）以F为原点，FG为x轴，FE为y轴，FA1为z轴，建立空间直角坐标系，利用向量法能求出点B到平面A1EG的距离．
边长为2的正三角形ABC中，点D，E，G分别是边AB，AC，BC的中点，
连接DE，连接AG交DE于点F．
，
平面
，
平面，
平面．
将
沿DE折叠至
的位置，使得平面
平面BCED，连接
，EG．
以F为原点，FG为x轴，FE为y轴，
为z轴，建立空间直角坐标系，
1，
，
0，
，
，
0，，
，
，
，
设平面
的法向量
y，
，
则
，取
，得
，
点B到平面的距离
．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
