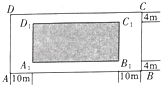
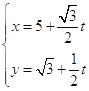题目内容
【题目】△ABC的内角A、B、C的对边分别为a、b、c,已知![]() .
.
(1)求角C;(2)若c=2![]() ,求△ABC的面积S的最大值.
,求△ABC的面积S的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)已知等式利用正弦定理化简,整理后根据sinA不为0求出cosC的值,进而确定出sinC的值;
(2)由cosC,c的值,利用余弦定理列出关系式,再利用基本不等式求出ab的最大值,即可确定出S的最大值.
试题解析:
(1)∵2a=![]() csinA﹣acosC,
csinA﹣acosC,
∴由正弦定理可得:2sinA=![]() sinCsinA﹣sinAcosC,
sinCsinA﹣sinAcosC,
∵sinA≠0,
∴可得:2=![]() sinC﹣cosC,解得:sin(C﹣
sinC﹣cosC,解得:sin(C﹣![]() )=1,
)=1,
∵C∈(0,π),可得:C﹣![]() ∈(﹣
∈(﹣![]() ,
,![]() ),
),
∴C﹣![]() =
=![]() ,可得:C=
,可得:C=![]() .
.
(2)∵由(1)可得:cosC=﹣![]() ,
,
∴由余弦定理,基本不等式可得:12=b2+a2+ab≥3ab,即:ab≤4,(当且仅当b=a时取等号)
∴S△ABC=![]() absinC=
absinC=![]() ab≤
ab≤![]() ,可得△ABC面积的最大值为
,可得△ABC面积的最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目