题目内容
【题目】随着我市九龙江南岸江滨路建设的持续推进，未来市民将新增又一休闲好去处，据悉南江滨路建设工程规划配套建造一个长方形公园ABCD，如图所示，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成，已知休闲区A1B1C1D1的面积为4000m2 ， 人行道的宽度分别为4m和10m．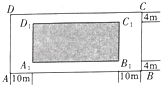
（1）若休闲区的长A1B1=x m，求公园ABCD所占面积S关于x的函数S（x）的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？
【答案】
（1）解：由A1B1=x米，知B1C1= 
米
∴S=（x+20）（ +8）=4160+8x+ 
（x＞0）
（2）解：S=4160+8x+ ≥4160+2 
=5760
当且仅当8x= ，即x=100时取等号
∴要使公园所占面积最小，休闲区A1B1C1D1的长为100米、宽为40米
【解析】（1）利用休闲区A1B1C1D1的面积为4000平方米，表示出B1C1= 米进而可得公园ABCD所占面积S关于x的函数S（x）的解析式；（2）利用基本不等式确定公园所占最小面积，即可得到结论
【考点精析】关于本题考查的基本不等式和基本不等式在最值问题中的应用，需要了解基本不等式：
,（当且仅当
时取到等号）；变形公式：
；用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能得出正确答案．
练习册系列答案
初中学业考试导与练系列答案
相关题目
