题目内容
【题目】已知直线 
： 
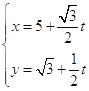（t为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的坐标方程为 
．
（1）将曲线C的极坐标方程化为直坐标方程；
（2）设点M的直角坐标为 
，直线l与曲线C的交点为A，B，求|MA||MB|的值．
【答案】
（1）解：∵ ，∴ 
，∴ ，故它的直角坐标方程为 ；
（2）解：直线 
： 
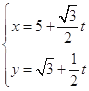（t为参数），普通方程为 ， 在直线 上，过点M作圆的切线，切点为T，则 ，由切割线定理，可得 ．
【解析】分析：本题主要考查了直线的参数方程，解决问题的关键是第一问，曲线的极坐标方程即 ，根据极坐标和直角坐标的互化公式 
、 
、 
，得x2+y2=2x，即得它的直角坐标方程；第二问，直线 的方程经过消参转化为普通方程，再利用切割线定理可得结论．
【考点精析】本题主要考查了直线的参数方程的相关知识点，需要掌握经过点
，倾斜角为
的直线
的参数方程可表示为
（
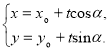为参数）才能正确解答此题．
练习册系列答案
相关题目
