Question

【题目】如图1,在正方形中，是的中点，点在线段上,且.若将 分别沿折起，使两点重合于点,如图2.

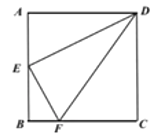
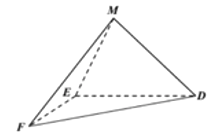
图1 图2

(1)求证:平面；

(2)求直线与平面所成角的正弦值.

Answer 1

【答案】(1)证明见解析；(2).

【解析】

（1）设正方形的边长为，由，可得，结合，利用线面垂直的判定定理，即可得到平面.

（2）建立空间直角坐标系，过点作，垂足为，求出向量和平面的一个法向量，利用向量的夹角公式，即可求解.

（1）证明：设正方形的边长为4，由图1知,,

, ,

,,即

由题意知，在图2中，,,平面,平面,且,

平面,平面,.

又平面,平面,且,平面

（2）由（1）知平面，则建立如图所示空间直角坐标系，过点作，垂足为，

在中，, ,从而

,,,

,,.

设平面的一个法向量为，则，

令，则，，.设直线与平面所成角为,

则, .直线与平面所成角的正弦值为..