题目内容
【题目】已知实数
满足
，若
只在点（4，3）处取得最大值，则
的取值范围是
A. 
B. 
C. 
D. 
【答案】C
【解析】
由约束条件作出可行域，然后对a进行分类，当a≥0时显然满足题意，当a＜0时，化目标函数为直线方程斜截式，比较其斜率与直线BC的斜率的大小得到a的范围．
由不等式组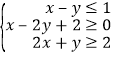
作可行域如图:
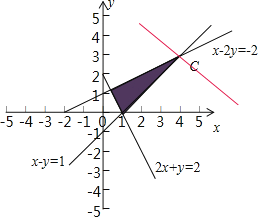
联立
，解得C（4，3）．
当a=0时，目标函数化为z=x，由图可知，
可行解（4，3）使z=x﹣ay取得最大值，符合题意；
当a＞0时，由z=x﹣ay，得y=
x
，此直线斜率大于0，当在y轴上截距最大时z最大，
可行解（4，3）为使目标函数z=x﹣ay的最优解，
a＜1符合题意；
当a＜0时，由z=x﹣ay，得y=x，此直线斜率为负值，
要使可行解（4，3）为使目标函数z=x﹣ay取得最大值的唯一的最优解，则＜0，即a＜0．
综上，实数a的取值范围是（﹣∞，1）．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某工厂的某车间共有
位工人，其中
的人爱好运动。经体检调查，这位工人的健康指数（百分制）如下茎叶图所示。体检评价标准指出：健康指数不低于
者为“身体状况好”，健康指数低于者为“身体状况一般”。
（1）根据以上资料完成下面的
列联表，并判断有多大把握认为“身体状况好与爱好运动有关系”？
身体状况好 | 身体状况一般 | 总计 | |
爱好运动 | |||
不爱好运动 | |||
总计 |
|
（2）现将位工人的健康指数分为如下
组：
，
，
，
，
，其频率分布直方图如图所示。计算该车间中工人的健康指数的平均数，由茎叶图得到真实值记为
，由频率分布直方图得到估计值记为
，求与的误差值；
（3）以该车间的样本数据来估计该厂的总体数据，若从该厂健康指数不低于者中任选
人，设
表示爱好运动的人数，求的数学期望。
附：
。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
