题目内容
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分别在直角三角形中求出![]() 和
和![]() ,然后根据
,然后根据![]() 可求出最后结果;(2)当投影的图像最清晰时,幕墙EF的高度最小,即求
可求出最后结果;(2)当投影的图像最清晰时,幕墙EF的高度最小,即求![]() 的最小值,利用两角差的正切函数公式与基本不等式相结合,可得最值.
的最小值,利用两角差的正切函数公式与基本不等式相结合,可得最值.
试题解析:(1)由AB=20m,CD=40m,BD=20m可得,∠CAG=![]() ,∠GAD=
,∠GAD=![]() ,
,
又投影设备的投影张角∠EAF为![]() ,所以
,所以![]() ,
,
所以G一定在EF上,所以![]() ,
,
所以![]() .
.
(2)当投影的图像最清晰时,幕墙EF的高度最小,即求y的最小值
由(1)得![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
又![]() ,所以满足题意,
,所以满足题意,
此时, ![]() .
.
答:当![]() 时,投影的图像最清晰,此时幕墙EF的高度为
时,投影的图像最清晰,此时幕墙EF的高度为![]() m.
m.

【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式: 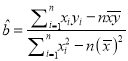 ,
, ![]() )
)