题目内容
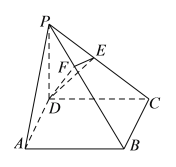
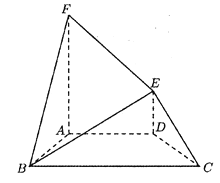
【题目】如图,在直角梯形ABCD中,AD∥BC, AB⊥BC, BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE, AC, DE,得到如图所示的空间几何体.


(1)求证:AB⊥平面ADC;
(2)若AD=1,AB=![]() ,求点B到平面ADE的距离.
,求点B到平面ADE的距离.
【答案】(1)证明见解析.
(2) ![]() .
.
【解析】分析:(1)证明DC⊥AB,AD⊥AB,即可得到AB⊥平面ADC.
(2)因为AB=![]() ,AD=1,所以BD=
,AD=1,所以BD=![]() ,依题意△ABD∽△DCB,得到CD=
,依题意△ABD∽△DCB,得到CD=![]() ,利用等体积法即可.
,利用等体积法即可.
详解:(1)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又BD⊥DC,DC平面BCD,所以DC⊥平面ABD.
因为AB平面ABD,所以DC⊥AB.
又AD⊥AB,DC∩AD=D,AD,DC平面ADC,所以AB⊥平面ADC.
(2)因为AB=![]() ,AD=1,所以BD=
,AD=1,所以BD=![]() .
.
依题意△ABD∽△DCB,所以![]() =
=![]() ,即
,即![]() =
=![]() .
.
所以CD=![]() .
.
故BC=3.
由于AB⊥平面ADC,AB⊥AC,E为BC的中点,
所以AE=![]() =
=![]() .
.
同理DE=![]() =
=![]() .
.
所以S△ADE=![]() ×1×
×1×![]() =
=![]() .
.
因为DC⊥平面ABD,
所以VA—BCD=![]() CD·S△ABD=
CD·S△ABD=![]() .
.
设点B到平面ADE的距离为d,
则![]() d·S△ADE=VB—ADE=VA—BDE=
d·S△ADE=VB—ADE=VA—BDE=![]() VA—BCD=
VA—BCD=![]() ,
,
所以d=![]() ,即点B到平面ADE的距离为
,即点B到平面ADE的距离为![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】兰天购物广场某营销部门随机抽查了100名市民在2018年国庆长假期间购物广场的消费金额,所得数据如表,已知消费金额不超过3千元与超过3千元的人数比恰为![]() .
.
消费金额(单位:千元) | 人数 | 频率 |
| 8 | 0.08 |
| 12 | 0.12 |
|
|
|
|
|
|
| 8 | 0.08 |
| 7 | 0.07 |
合计 | 100 | 1.00 |

(1)试确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(2)用分层抽样的方法从消费金额在![]() 、
、![]() 和
和![]() 的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?