题目内容
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
【答案】(1)![]() .(2)见解析。
.(2)见解析。
【解析】试题分析:(1)根据![]() ,
, ![]() 两点关于y轴对称,由椭圆的对称性可知C经过
两点关于y轴对称,由椭圆的对称性可知C经过![]() ,
, ![]() 两点.另外由
两点.另外由![]() 知,C不经过点P1,所以点P2在C上.因此
知,C不经过点P1,所以点P2在C上.因此![]() 在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l:
在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l: ![]() (
(![]() ),将
),将![]() 代入
代入![]() ,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出
,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出![]() ,根据
,根据![]() 列出等式表示出
列出等式表示出![]() 和
和![]() 的关系,从而判断出直线恒过定点.
的关系,从而判断出直线恒过定点.
试题解析:(1)由于![]() ,
, ![]() 两点关于y轴对称,故由题设知C经过
两点关于y轴对称,故由题设知C经过![]() ,
, ![]() 两点.
两点.
又由![]() 知,C不经过点P1,所以点P2在C上.
知,C不经过点P1,所以点P2在C上.
因此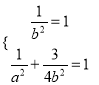 ,解得
,解得![]() .
.
故C的方程为![]() .
.
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知![]() ,且
,且![]() ,可得A,B的坐标分别为(t,
,可得A,B的坐标分别为(t, ![]() ),(t,
),(t, ![]() ).
).
则![]() ,得
,得![]() ,不符合题设.
,不符合题设.
从而可设l: ![]() (
(![]() ).将
).将![]() 代入
代入![]() 得
得
![]()
由题设可知![]() .
.
设A(x1,y1),B(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
而![]()
![]()
![]() .
.
由题设![]() ,故
,故![]() .
.
即![]() .
.
解得![]() .
.
当且仅当![]() 时,
时, ![]() ,欲使l:
,欲使l: ![]() ,即
,即![]() ,
,
所以l过定点(2, ![]() )
)
点睛:椭圆的对称性是椭圆的一个重要性质,判断点是否在椭圆上,可以通过这一方法进行判断;证明直线过定点的关键是设出直线方程,通过一定关系转化,找出两个参数之间的关系式,从而可以判断过定点情况.另外,在设直线方程之前,若题设中未告知,则一定要讨论直线斜率不存在和存在两种情况,其通法是联立方程,求判别式,利用根与系数的关系,再根据题设关系进行化简.

【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如表:
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
资金 | 单位产品所需资金(百元) | ||
空调机 | 洗衣机 | 月资金供应量(百元) | |
成本 | 30 | 20 | 300 |
劳动力(工资) | 5 | 10 | 110 |
单位利润 | 6 | 8 | |