题目内容
.函数y=(2x＋1)3在x=0处的导数是
| A．0 | B．1 |
| C．3 | D．6 |
D
本题考查常见函数的导数及其运算法则.应先将其转化成f(x)=a0xn＋a1xn－1＋…＋an－1x＋an的形式，再求导.也可用复合函数求导法则.
解法一:∵y=(2x＋1)3=(2x)3＋3·(2x)2＋3·(2x)＋1=8x3＋12x2＋6x＋1,
∴y′=24x2＋24x＋6.∴y′|x=0=6.
解法二:∵y=(2x＋1)3,∴y′=3(2x＋1)2·(2x＋1)=6(2x＋1)2.
∴y′|x=0=6.
解法一:∵y=(2x＋1)3=(2x)3＋3·(2x)2＋3·(2x)＋1=8x3＋12x2＋6x＋1,
∴y′=24x2＋24x＋6.∴y′|x=0=6.
解法二:∵y=(2x＋1)3,∴y′=3(2x＋1)2·(2x＋1)=6(2x＋1)2.
∴y′|x=0=6.
练习册系列答案
相关题目
)
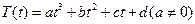，其中温度的单位是℃，时间的单位是小时．中午12:00相应的t=0，中午12:00以后相应的t取正数，中午12:00以前相应的t取负数（如早上8：00相应的t=-4，下午16：00相应的t=4）．若测得该物体在早上8:00的温度为8℃，中午12:00的温度为60℃，下午13:00的温度为58℃，且已知该物体的温度早上8:00与下午16:00有相同的变化率.
－
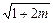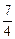+cos2x)对任意x∈R都成立，求实数m的取值范围.
在
处的导数。