题目内容
.已知f(x)=x3＋ax2＋(a＋6)x＋1有极大值和极小值，则a的范围为
| A．－1＜a＜2 | B．－3＜a＜6 |
| C．a＜－1或a＞2 | D．a＜－3或a＞6 |
D
本题考查常见函数的导数及其应用.要使f(x)有极大值与极小值，需使方程f′(x)=0有两个不相等的实数根.
f′(x)=3x2＋2ax＋(a＋6).
要使方程f′(x)=3x2＋2ax＋(a＋6)=0有两个不相等的实数根，只需
Δ=(2a)2－4×3×(a＋6)＞0,
即a2－3a－18＞0,得a＜－3或a＞6.
f′(x)=3x2＋2ax＋(a＋6).
要使方程f′(x)=3x2＋2ax＋(a＋6)=0有两个不相等的实数根，只需
Δ=(2a)2－4×3×(a＋6)＞0,
即a2－3a－18＞0,得a＜－3或a＞6.
练习册系列答案
相关题目
，则f（2009）的值为( )
时整，甲船自
处以
的速度向正东行驶，乙船自
处以
分时两船之间距离对时间的变化率是_____________.
时的速度为
，则该车在
时的加速度为（ ）
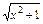在x0到x0+Δx之间的平均变化率.