题目内容
(12分) 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且MD= PD.
PD.

(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为 的直线被C所截线段的长度.
的直线被C所截线段的长度.
 PD.
PD.
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为
 的直线被C所截线段的长度.
的直线被C所截线段的长度.(1) +
+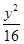 =1.(2)AB=
=1.(2)AB= .
.
 +
+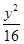 =1.(2)AB=
=1.(2)AB= .
.试题分析:设M的坐标为(x,y),P的坐标为(xP,yP),然后利用MD=
 PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.
PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.(1)设M的坐标为(x,y),P的坐标为(xP,yP),
由已知得
 ∵P在圆上,
∵P在圆上,∴x2+(
 y)2=25,
y)2=25,即轨迹C的方程为
 +
+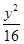 =1.
=1.(2)过点(3,0)且斜率为
 的直线方程为y=
的直线方程为y= (x-3),
(x-3),设直线与C的交点为A(x1,y1),B(x2,y2),将直线方程y=
 (x-3)代入C的方程,
(x-3)代入C的方程,得
 +
+ =1,即x2-3x-8=0.
=1,即x2-3x-8=0.∴x1=
 ,x2=
,x2= .
.∴线段AB的长度为
AB=

=

=
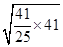 =
= .
.点评:本小题属于相关点法求轨迹方程要把主动点的坐标用被动点的坐标表示出来,然后再代入主动点所在曲线的方程即可求出动点的轨迹方程.在涉及直线与椭圆相交求弦长时要借助韦达定理及弦长公式,一般不考虑求交点坐标.

练习册系列答案
相关题目
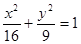 的焦距是 ,焦点坐标为
的焦距是 ,焦点坐标为  的左右焦点分别为
的左右焦点分别为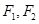 ,过焦点
,过焦点 的直线交该椭圆于
的直线交该椭圆于 两点,若
两点,若 的内切圆面积为
的内切圆面积为 ,
, ,则
,则 的值为 。
的值为 。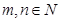 ,且点A
,且点A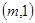 和点B
和点B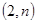 都在椭圆
都在椭圆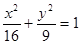 内部,
内部,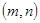 的所有可能结果;
的所有可能结果;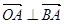 成立的
成立的 被椭圆
被椭圆 所截得的弦的中点坐标是( )
所截得的弦的中点坐标是( ) ,
, 
 ,
,  ,
,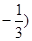
 ,
, 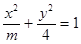 ,对于任意实数
,对于任意实数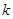 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线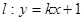 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )

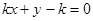


 经过点
经过点 ,一个焦点是
,一个焦点是 .
. 的方程;
的方程; 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 、
、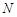 两点.试问:当点
两点.试问:当点 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.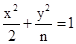 的离心率为
的离心率为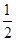 ,则n=( )
,则n=( )



 上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____;
上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____;