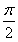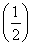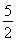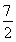题目内容
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
A.b>a>c B.c>a>b
C.c>b>a D.a>c>b
A
【解析】因为函数y=f(x)关于y轴对称,所以函数y=xf(x)为奇函数.因为[xf(x)]′=f(x)+xf′(x),且当x∈(-∞,0)时,[xf(x)]′=f(x)+xf′(x)<0,则函数y=xf(x)在(-∞,0)上单调递减;因为y=xf(x)为奇函数,所以当x∈(0,+∞)时,函数y=xf(x)单调递减.因为1<20.2<2,0<logπ3<1,log39=2,所以0<logπ3<20.2<log39,所以b>a>c,选A.

练习册系列答案
相关题目