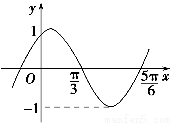
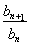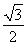题目内容
已知各项均为正数的数列{an}的前n项和为Sn,满足8Sn=a+4an+3(n∈N*),且a1,a2,a7依次是等比数列{bn}的前三项.
(1)求数列{an}及{bn}的通项公式;
(2)是否存在常数a>0且a≠1,使得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
(1)an=4n-3,bn=5n-1.(2)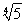
【解析】(1)n=1时,8a1=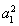 +4a1+3,a1=1或a1=3.(2分)
+4a1+3,a1=1或a1=3.(2分)
当n≥2时,8Sn-1= +4an-1+3,
+4an-1+3,
an=Sn-Sn-1=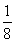 (
( +4an-
+4an- -4an-1),
-4an-1),
从而(an+an-1)(an-an-1-4)=0
因为{an}各项均为正数,所以an-an-1=4.(6分)
所以,当a1=1时,an=4n-3;当a1=3时,an=4n-1.
又因为当a1=1时,a1,a2,a7分别为1,5,25,构成等比数列,
所以an=4n-3,bn=5n-1.
当a1=3时,a1,a2,a7分别为3,7,27,不构成等比数列,舍去.(11分)
(2)假设存在a,理由如下:(12分)
由(1)知,an=4n-3,bn=5n-1,从而
an-lonabn=4n-3-loga5n-1=4n-3-(n-1)·loga5=(4-loga5)n-3+loga5.
由题意,得4-loga5=0,所以a=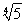 .(16分)
.(16分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目