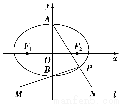
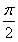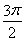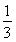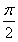ЬтФПФкШн
ЩшКЏЪ§f(x)ЕФЖЈвхгђЮЊDЃЌШєДцдкЗЧСуЪЕЪ§lЪЙЕУЖдгкШЮвтxЁЪM(M⊆D)ЃЌгаxЃЋlЁЪDЃЌЧвf(xЃЋl)Ёнf(x)ЃЌдђГЦКЏЪ§f(x)ЮЊMЩЯЕФlИпЕїКЏЪ§ЃЎЯжИјГіЯТСаУќЬтЃК
ЂйКЏЪ§f(x)ЃН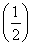 xЪЧRЩЯЕФ1ИпЕїКЏЪ§ЃЛ
xЪЧRЩЯЕФ1ИпЕїКЏЪ§ЃЛ
ЂкКЏЪ§f(x)ЃНsin 2xЮЊRЩЯЕФІаИпЕїКЏЪ§ЃЛ
ЂлШчЙћЖЈвхгђЮЊ[Ѓ1ЃЌЃЋЁо)ЕФКЏЪ§f(x)ЃНx2ЮЊ[Ѓ1ЃЌЃЋЁо)ЩЯЕФmИпЕїКЏЪ§ЃЌФЧУДЪЕЪ§mЕФШЁжЕЗЖЮЇЪЧ[2ЃЌЃЋЁо)ЃЎ
Цфжае§ШЗЕФУќЬтЪЧ________ЃЎ(аДГіЫљгае§ШЗУќЬтЕФађКХ)
ЂкЃЌЂл
ЁОНтЮіЁПЖдгкЂйЃЌЁпxЁЪRЃЌЁрxЃЋ1ЁЪR.
гжf(x)ЃН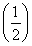 xдкRЩЯЪЧМѕКЏЪ§ЃЌ
xдкRЩЯЪЧМѕКЏЪ§ЃЌ
Ёр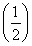 xЃЋ1ЃМ
xЃЋ1ЃМ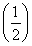 xЃЌМДf(xЃЋ1)ЃМf(x)ЃЎЁрЂйДэЃЎ
xЃЌМДf(xЃЋ1)ЃМf(x)ЃЎЁрЂйДэЃЎ
ЖдгкЂкЃЌЁпxЁЪRЃЌЁрxЃЋІаЁЪR.
Ёрf(xЃЋІа)ЃНsin 2(xЃЋІа)ЃНsin 2xЃНf(x)ЃЎЁрЂке§ШЗЃЎ
ЖдгкЂлЃЌЁпf(x)ЃНx2ЮЊ[Ѓ1ЃЌЃЋЁо)ЩЯЕФmИпЕїКЏЪ§ЃЌ
Ёрf(xЃЋm)Ёнf(x)МД(xЃЋm)2Ёнx2ЃЌ
Ёр2mxЃЋm2Ён0ЖдгкxЁЪ[Ѓ1ЃЌЃЋЁо)КуГЩСЂЃЎ
Ёр Лђ
Лђ .ЁрmЁн2ЃЌМДЂле§ШЗЃЎ
.ЁрmЁн2ЃЌМДЂле§ШЗЃЎ
Ёре§ШЗУќЬтЪЧЂкЃЌЂл

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП