题目内容
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.(1) 证明:
构成等比数列.(1) 证明: ;(2) 求数列
;(2) 求数列 的通项公式;(3) 证明:对一切正整数
的通项公式;(3) 证明:对一切正整数 ,有
,有 .
.
 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.(1) 证明:
构成等比数列.(1) 证明: ;(2) 求数列
;(2) 求数列 的通项公式;(3) 证明:对一切正整数
的通项公式;(3) 证明:对一切正整数 ,有
,有 .
.(1)证明见解析;(2) ;(3)证明见解析.
;(3)证明见解析.
 ;(3)证明见解析.
;(3)证明见解析.试题分析:(1)对于
 取n=1,可得到
取n=1,可得到 与
与 的关系,即可证得;(2)当
的关系,即可证得;(2)当 时,有
时,有 ,可得到的
,可得到的 与
与 的关系式,从而可知等差数列
的关系式,从而可知等差数列 的公差,又由
的公差,又由 构成等比数列,从而可求出基本量
构成等比数列,从而可求出基本量 ,即可写出其通项公式;(3)裂项:
,即可写出其通项公式;(3)裂项: ,以下用裂项相消法,即可化简题中左式,从而证得不等式.
,以下用裂项相消法,即可化简题中左式,从而证得不等式.试题解析:(1)当
 时,
时, ,
, ;
;(2)当
 时,
时, ,
, ;
; ,
, ,
, 当
当 时,
时, 是公差
是公差 的等差数列.
的等差数列. 构成等比数列,
构成等比数列, ,
, ,解得
,解得 ,由(1)可知,
,由(1)可知, ,
,

 是首项
是首项 ,公差
,公差 的等差数列.
的等差数列. 数列
数列 的通项公式为
的通项公式为 .
.(3)


 与
与 的关系:
的关系: ,等差数列的定义,等比中项,裂项相消求和法,特殊到一般思想,化归思想.
,等差数列的定义,等比中项,裂项相消求和法,特殊到一般思想,化归思想.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,其中
成等差数列,其中 .
. 满足:
满足: ,记数列
,记数列 ,求
,求 的最大项.
的最大项. 中,前
中,前 项和
项和 ,若
,若 ,
, ,则
,则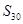 = .
= . ,则
,则 的值为( ).
的值为( ).


