题目内容
已知f(x)=sin(2x+
)+cos(2x-
).
(Ⅰ)求f(x)的最大值及取得最大值时x的值;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(C)=1,c=2
,sinA=2sinB,求△ABC的面积.
| π |
| 6 |
| π |
| 3 |
(Ⅰ)求f(x)的最大值及取得最大值时x的值;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(C)=1,c=2
| 3 |
(Ⅰ)f(x)=
sin2x+
cos2x+
cos2x+
sin2x=
sin2x+cos2x=2sin(2x+
),
当2x+
=2kπ+
,即x=kπ+
,k∈Z时,函数f(x)取得最大值2;
(Ⅱ)由f(C)=2sin(2C+
)=1,得sin(2C+
)=
,
∵
<2C+
<2π+
,
∴2C+
=
,解得C=
,
∵sinA=2sinB,
∴根据正弦定理,得a=2b,
∴由余弦定理,有c2=a2+b2-2abcosC,即12=4b2+b2-2b2=3b2,
解得:b=2,a=4,
则S△ABC=
absinC=
×4×2×sin
=2
.
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
(Ⅱ)由f(C)=2sin(2C+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∵
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴2C+
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
∵sinA=2sinB,
∴根据正弦定理,得a=2b,
∴由余弦定理,有c2=a2+b2-2abcosC,即12=4b2+b2-2b2=3b2,
解得:b=2,a=4,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.(1) 证明:
构成等比数列.(1) 证明: ;(2) 求数列
;(2) 求数列 .
.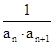 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值. >0,则a2014= ( )
>0,则a2014= ( )