题目内容
已知曲线y＝x3＋1，求过点P(1,2)的曲线的切线方程．
3x－y－1＝0或3x－4y＋5＝0.
设切点为A(x0，y0)，则y0＝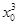
＋1.
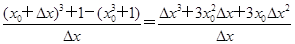＝Δx2＋3x0Δx＋3
.
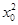∴f′(x0)＝3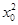，切线的斜率为k＝3.
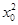点(1,2)在切线上，∴2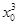－(＋1)＝3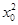 (1－x0)．∴x0＝1或x0＝－
.
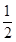当x0＝1时，切线方程为3x－y－1＝0，
当x0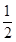＝－时，切线方程为3x－4y＋5＝0.
所以，所求切线方程为3x－y－1＝0或3x－4y＋5＝0.
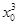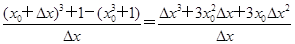＋1.＝Δx2＋3x0Δx＋3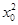.∴f′(x0)＝3
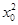，切线的斜率为k＝3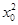.点(1,2)在切线上，∴2－(
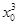＋1)＝3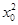 (1－x0)．∴x0＝1或x0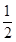＝－.当x0＝1时，切线方程为3x－y－1＝0，
当x0＝－
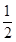时，切线方程为3x－4y＋5＝0.所以，所求切线方程为3x－y－1＝0或3x－4y＋5＝0.
练习册系列答案
黎明文化寒假作业系列答案
相关题目
在
处的切线方程是（ ）
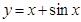在点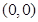
处的切线方程是 .
在点P(3,1)处的切线斜率为 ( )．