题目内容
若曲线y＝x2－1的一条切线平行于直线y＝4x－3，则这条切线方程为_____________．
4x－y－5＝0
∵f′(x)＝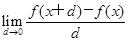
＝
＝
＝
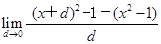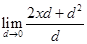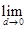(2x＋d)＝2x.
设切点坐标为(x0，y0)，则由题意知f′(x0)＝4，即2x0＝4，∴x0＝2，代入曲线方程得y0＝3，故该切线过点(2,3)且斜率为4.所以这条切线方程为y－3＝4(x－2)，即4x－y－5＝0.
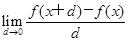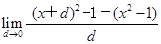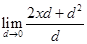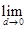＝＝＝ (2x＋d)＝2x.设切点坐标为(x0，y0)，则由题意知f′(x0)＝4，即2x0＝4，∴x0＝2，代入曲线方程得y0＝3，故该切线过点(2,3)且斜率为4.所以这条切线方程为y－3＝4(x－2)，即4x－y－5＝0.
练习册系列答案
名校课堂系列答案
相关题目
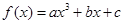图像过点
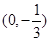，且在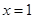
处的切线方程是
.
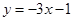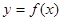的解析式；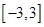
上的最大值和最小值．
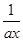+b(a>0).
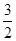x,求a,b的值.
，则切点坐标为________．
gt2，则从t＝0到t＝1时间段内的平均速度为________，在t＝1到t＝1＋Δt时间段内的平均速度________，在t＝1时刻的瞬时速度为________．