Question

【题目】已知四边形为矩形, ,为的中点,将沿折起,得到四棱锥,设的中点为,在翻折过程中,得到如下有三个命题:

①平面，且的长度为定值；

②三棱锥的最大体积为；

③在翻折过程中，存在某个位置，使得.

其中正确命题的序号为__________．（写出所有正确结论的序号）

Answer 1

【答案】①②

【解析】

取的中点，连接、，证明四边形为平行四边形，得出，可判断出命题①的正误；由为的中点，可知三棱锥的体积为三棱锥

的一半，并由平面平面，得出三棱锥体积的最大值，可判断出命题②的正误；取的中点，连接，由，结合得出平面，推出得出矛盾，可判断出命题③的正误.

如下图所示：

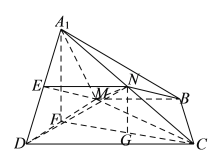
对于命题①，取的中点，连接、，则，，

，由勾股定理得，

易知，且，、分别为、的中点，所以，，

四边形为平行四边形，，，

平面，平面，平面，命题①正确；

对于命题②，由为的中点，可知三棱锥的体积为三棱锥的一半，当平面平面时，三棱锥体积取最大值，

取的中点，则，且，

平面平面，平面平面，，

平面，平面，

的面积为，

所以，三棱锥的体积的最大值为，

则三棱锥的体积的最大值为，命题②正确；

对于命题③，，为的中点，所以，，

若，且，平面，

由于平面，，事实上，易得，，

，由勾股定理可得，这与矛盾，命题③错误.

故答案为：①②.