题目内容
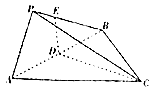
【题目】在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,已知a=![]() c.
c.
(1)若∠A=2∠B,求cosB;
(2)若AC=2,求△ABC面积的最大值.
【答案】(1)cos B=![]() .(2)△ABC面积最大为2
.(2)△ABC面积最大为2![]() .
.
【解析】分析:(1)由题意结合正弦定理可得![]() =
=![]() =
=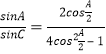 ,则cos
,则cos![]() =
=![]() ,∠A=
,∠A=![]() ,cos B=
,cos B=![]() .
.
(2)由题意结合余弦定理和面积公式可得S![]() +8,结合二次函数的性质可知△ABC面积最大为2
+8,结合二次函数的性质可知△ABC面积最大为2![]() .
.
详解:(1)在△ABC中,∠A=2∠B,∠C=![]() -
-![]() 且∠A∈(0,
且∠A∈(0,![]() ),
),
由正弦定理![]() =
=![]() =
=![]() ,
,
=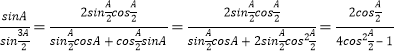 ,
,
解方程4cos2![]() -
-![]() cos
cos![]() -1=0得cos
-1=0得cos![]() =
=![]() (舍负),
(舍负),
所以,∠A=![]() ,所以cos B=
,所以cos B=![]() .
.
(2)cos B=![]() =
=![]() ,
,
S![]() (
(![]() ac sinB)2=
ac sinB)2=![]() a2c2sin2B,
a2c2sin2B,
=![]() a2c2(1-cos2B)=
a2c2(1-cos2B)=![]() ×2c4×
×2c4×![]() =
=![]() +8,
+8,
所以当c2=12即c=2![]() 时,S
时,S![]() 取得最大值为8,此时S
取得最大值为8,此时S![]() 2
2![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
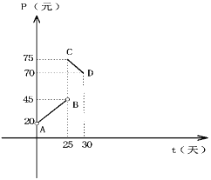
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)