Question

【题目】已知一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1，x2，且0<x1<1,x2>1,则 的取值范围是( )
A.（-2，- ）
B.（-1，- ）
C.（-2， ）
D.（-1， ）

Answer 1

【答案】A
【解析】由方程x2+（1+a）x+1+a+b=0的二次项系数为1＞0，
故函数f（x）=x2+（1+a）x+1+a+b图象开口方向朝上，
又∵方程x2+（1+a）x+1+a+b=0的两根满足0＜x1＜1＜x2 ，
代入方程可得：
其对应的平面区域如下图阴影示：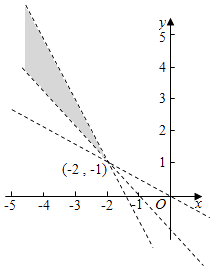

表示阴影区域上一点与原点边线的斜率，
由图可知 。
故答案为：A
由二次函数根的分布可得，f(0)和f(1)函数值的范围，将题目转化为可行域中点的斜率范围问题，利用数形结合的思想，即可求得范围。